What have satellite scheduling, the selected traveling salesperson (orienteering) problem, and make-to-order manufacturing in common?

First, these problems can all be modeled as a single-machine scheduling problem with release times, deadlines, time/sequence dependent setup times, and rejection, which is strongly NP-hard. Second, most instances are solved either best or fastest with one of our new algorithms! Some instances have been solved by us to optimality for the first time. Today the final open access version of our paper with an exact method for this has been made available online.

The figure below provides an example instance of this type of problem. It shows the release times, deadlines and processing times of all jobs in the input. The goal is then to select the largest set of jobs (or the set of jobs with the most value) such that no jobs are scheduled to be running at the same time. Only the time- and/or sequence-dependent setup times are not visualized here: this is an extra time needed between jobs, depending on when or after which other job it is scheduled. For the selected traveling salesperson problem (sometimes called the orienteering problem) this is the time needed to travel from one city to the next, for earth observation satellite scheduling this is the time needed to manoeuvre the satellite to the position of the next observation.

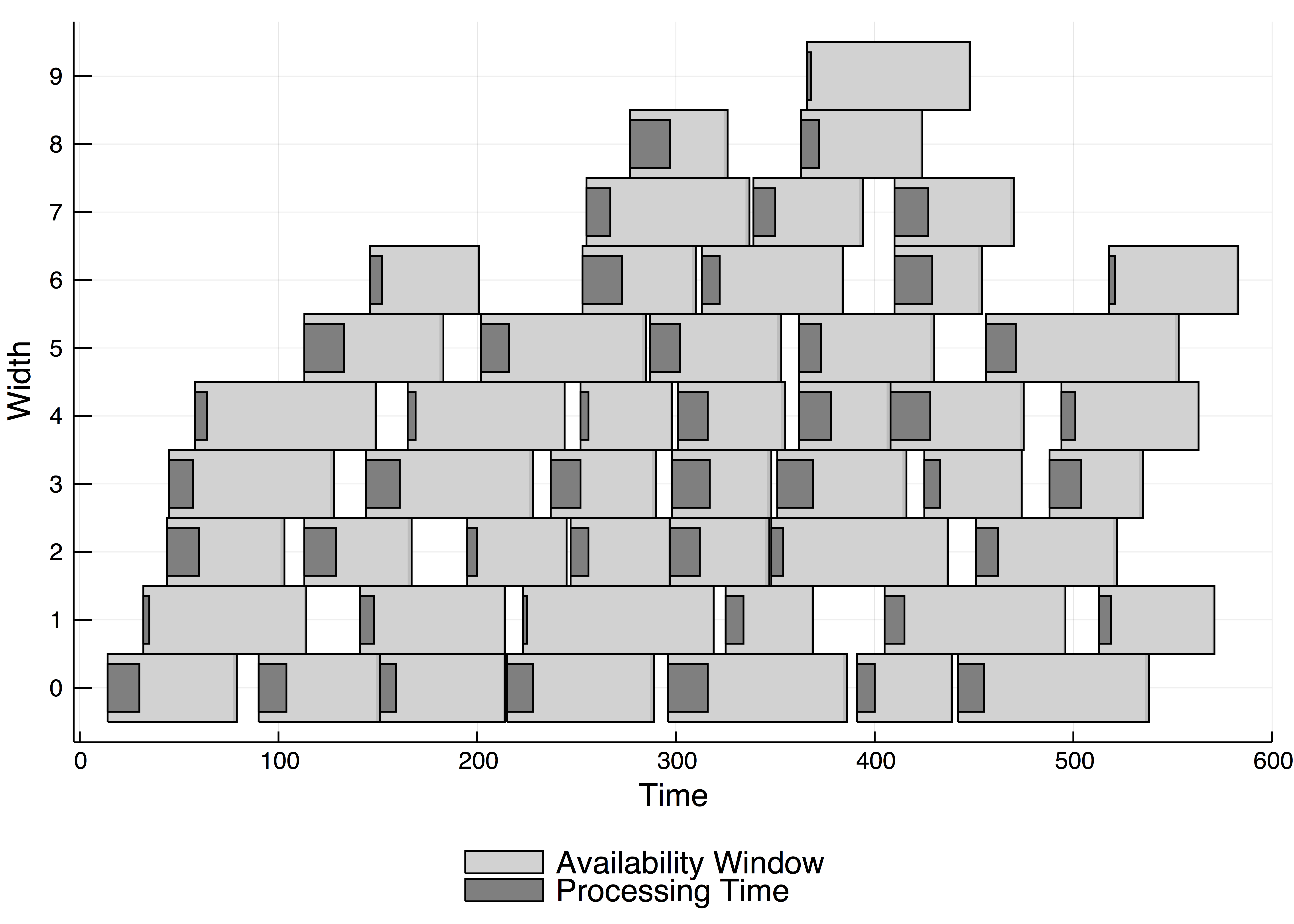
An example problem instance with 50 jobs: the grey bars indicate the time window in which the job can be scheduled, the dark grey bar the length of the job. The y-axis represents the number of jobs that could be scheduled at the same time (i.e. the width of the instance).

We have made two contributions towards heuristic algorithms and one on an exact method: we started by studying a genetic/memetic algorithm, where a population of solution (swarm) is iteratively improved. A recent successful one (BRKGA) used an encoding of the solutions where the order of the tasks is determined by an, initially random, key. We extended this approach with another successful approach, called adaptive large neighbourhood search (ALNS), which repeatedly makes several small modifications to a solution before accepting or rejecting it. We called our hybrid method Sparrow, after a bird known to fly in swarms. Sparrow obtained better solutions with comparable runtimes to the state of the art at the time. See our full publication for a detailed analysis of the performance under varying problem properties and on both standard and new benchmark instances. (Order Acceptance and Scheduling with Sequence-Dependent Setup Times: A new memetic algorithm and benchmark of the state of the art in Computers & Industrial Engineering 138 (2019), 10.1016/j.cie.2019.106102)

In our second heuristic algorithm we aimed at improving adaptive large neighbourhood search (ALNS) without using a swarm. We considered the inclusion of four algorithmic ideas: insertion, removal and instant tabu search, a new randomization strategy for neighbourhood operators, a partial sequence dominance heuristic, and a fast insertion strategy. A detailed factor analysis of the algorithmic features provided evidence that: (1) the insertion tabu and the removal tabu work better when the completion ratio is low, and the instant tabu works better when there are fewer jobs in the solution sequence; (2) the randomization strategy in the neighbourhood operators works well in terms of the solution quality and the running time; (3) the partial sequence dominance heuristic performs better when the problem instance grows in size, indicating that it helps to combine parts of different solutions, when the solution sequence gets long; and (4) the fast insertion strategy can insert a job at the best position in a solution with low runtime; of the four features, this one contributes the most to the performance, but also consumes more time compared with the other features. The combination of all four produces solutions with higher quality in less time than the state of the art. These results can be found in our paper Time/Sequence-Dependent Scheduling: The design and evaluation of a general purpose tabu-based adaptive large neighbourhood search algorithm (Journal of Intelligent Manufacturing 31 (2020), 10.1007/s10845-019-01518-4).

We believe generalizing these algorithms to other similar scheduling problems such as the multi-machine scheduling problem and the vehicle routing problem is relatively straightforward, since these novel techniques are applicable on such problems with similar sequencing and selecting properties.

Finally, and most recently, we published a novel algorithm for solving this NP-hard problem to optimality. This algorithm fits in the dynamic programming paradigm and can also be seen as a decision diagram. In particular the use of state dominance proved very effective. Interestingly, this method scales only quadratic in the number of jobs if the number of overlapping time windows and the slack are bounded. This algorithm has solved several standard benchmark instances with 100 jobs for which no optimal solution was ever reported in under an hour. Also we have shown how to use the algorithmic idea to inform an effective heuristic, inspired by the Balas neighborhood. Full details are available in our paper in the European Journal of Operational Research 291:2 (2021): Single-machine scheduling with release times, deadlines, setup times, and rejection, 10.1016/j.ejor.2020.09.042.

All the source codes and datasets used in these papers are available as open source: